Pseudoknot Removal Methods   Pseudoknots in RNA Structures Pseudoknots are RNA structures in which the base pairs are not fully nested. A pseudoknot exists when bases in a loop region pair with bases outside that loop region. For example, when any four bases occuring in the order A, B, C, D in an RNA sequence form base pairs (A, C) and (B, D) the structure is pseudoknotted. Pseudoknots cannot be expressed in the dot-bracket notation (i.e. the Vienna format). Pseudoknots are biologically important: they are known to be critical for the structure and function of many RNAs. Evolutionary conserved pseudoknots are involved in processes that include ribosomal frameshifting, self-cleavage, and self-splicing (see Staple and Butcher 2005 for a review). Pseudoknots cannot be handled by many computational procedures. Because of limitations in software or algorithms, it is often necessary to work with nested structures. To make a knotted structural model pseudoknot-free one or more base pairs must be "broken", treating the corresponding part of the sequence as unpaired. The complexity of this process is underestimated. Which criteria should be used to designate one group of base pairs as "the helix" and another group as "the pseudoknot"? In the RNA molecule there may be no physical distinction between the conflicting helices that make up a pseudoknot at a structural level. We have implemented a variety of algorithms for pseudoknot removal, each operating under different assumptions of what is important in the RNA structure. Most methods are available through this web interface. The full source code is available in the PyCogent library. A standalone implementation and a script for command-line control of the methods is available at the main page. 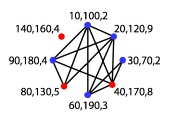Set of conflicting base pair regions in a pseudoknotted structure (black+red), and nested base pairs after pseudoknot removal using the Dynamic Programming approach (red).   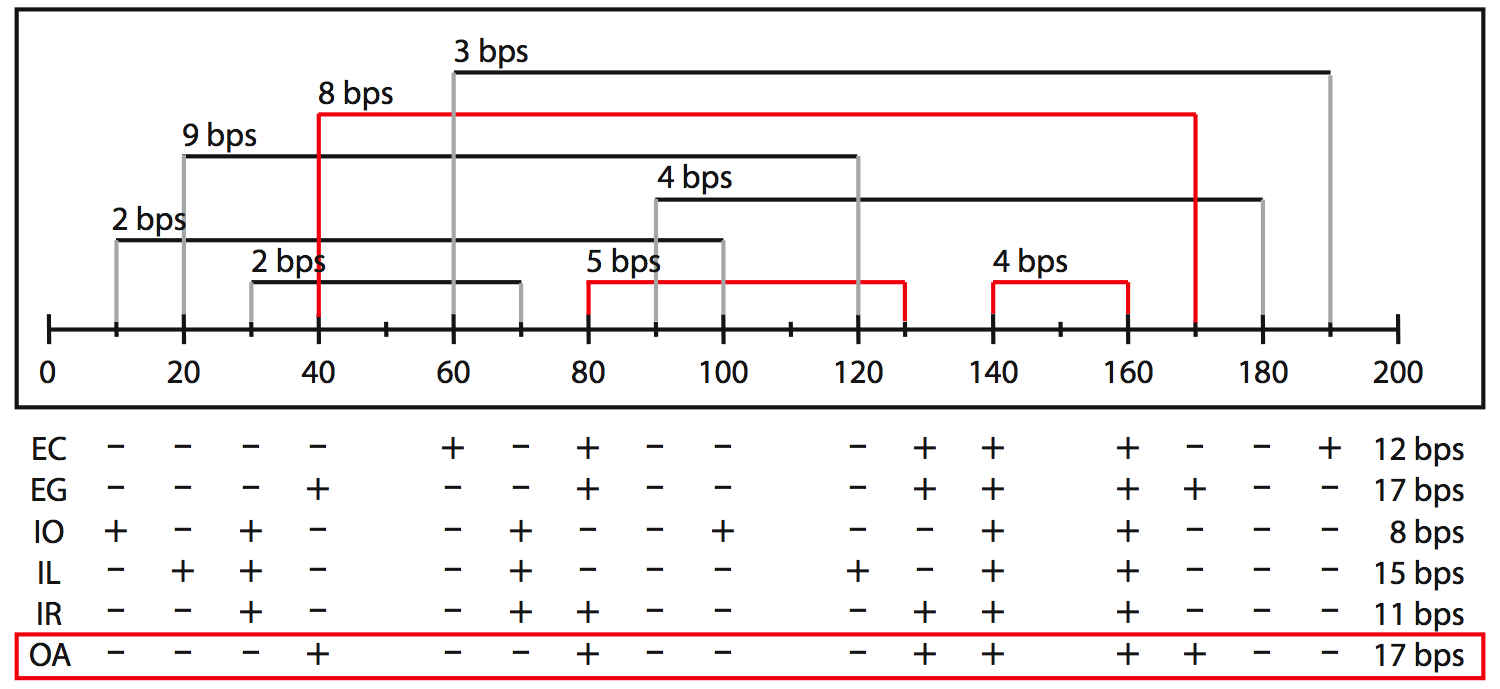Pseudoknot Removal Methods We have implemented several heuristics, which all use different rules to remove pseudoknots from an RNA structure, and an optimization approach that calculates all optimal solutions given some scoring function. All methods find saturated structures in which no base pair can be added without introducing a pseudoknot. All methods treat uninterrupted stretches of base pairs (paired regions) as a unit. Each paired region has a start, an end, and a length. The length of the region is the number of base pairs it contains. The range of a paired region is the distance between the highest upstream position and the lowest downstream position. For a region that conflicts with one or more other regions we can define the region's "gain" as the length of the region minus the cumulative length of all of its conflicting regions. It expresses how many base pairs are gained if this region is chosen and all of its conflicts have to be removed. Note that the gain of a region can be negative if all its conflicts together are longer (i.e. more base pairs) than itself. It is then preferable to remove this region in favor of its conflicts. Heuristics EC Elimination, Conflicts The EC method tries to reach a nested structure as fast as possible. It removes paired regions from the whole set beginning with the one with the most conflicts. In case two regions have an equal number conflicts, the region's gain and starting position are used to determine which region is processed first. This simple strategy might remove too many regions, resulting in an unsaturated structure, so optionally non-conflicting regions are added back. EG Elimination, Gain The EG heuristic eliminates conflicting paired regions on the basis of their "gain". The EG method processes the regions from the one with the smallest gain to the one with the largest gain (i.e. the most unfavorable regions are removed first). If two regions have the same gain, the number of conflicts and starting position are used to determine which region is processed first. To prevent finding unsaturated structures, this method adds back non-conflicting (see EC method). IO Incremental, Order The IO method starts with an empty list and adds paired regions that do not conflict with an already added region one by one. It takes the most simplistic approach, which is to add paired regions from the 5´ side to the 3´ side. IL Incremental, Length The IL method operates under the idea that longer regions are more important than shorter regions. Thus, it adds non-conflicting paired regions one by one, starting with the longest region and working towards the shortest region. In case of equal lengths, the region starting closest to the 5´ side is added first. IR Incremental, Range The IR method prefers short-range interactions over long range interactions, thus in this scenario the structure is built-up starting with the formation of the hairpin loops. Paired regions are added to the list from short to long-range. In case of equal ranges, the region starting closest to the 5´ end is added first. Optimization OA Optimization, All solutions The OA method calculates all nested structures that have an optimal score for some criterion. For example, one could maximize the number of base pairs or the number of hydrogen bonds. The OA method is a dynamic programming algorithm that efficiently calculates the optimal solutions from optimal sub-solutions. Through the web interface we only offer the scoring function that maximizes the number of base pairs, but in the source code any additive score function can be incorporated, possibly using sequence or alignment information. OSR Optimization, Single solution at Random This method calculates all optimal solutions with the OA method and returns one of them at random. OSP Optimization, Single solution by Properties This method calculates all optimal solutions with the OA method and returns one of them based on some properties of the optimal structures. The first criterion is the number of paired regions in the returned structure, the second is the average range of the regions, the third is the average start value of the regions. It returns the structure with the minimum value for these three properties.   When using our method, please cite: Sandra Smit, Kristian Rother, Jaap Heringa, and Rob Knight. (2008) From knotted to nested RNA structures: a variety of computational methods for pseudoknot removal. RNA 14(3):410-416. Copyright © 2007 Sandra Smit, Kristian Rother, Jaap Heringa, and Rob Knight